Optimization
- The base
R function for finding minima (the default) or maxima of functions of a single variable is optimize(). Eg:
> f <- function(x) {
+ x * (20 - 2 * x) * (16 - 2 * x)
+ }
>
> optimize(f, c(0, 8), maximum = TRUE)
## $maximum
## [1] 2.945
##
## $objective
## [1] 420.1
> g <- function(x) {
+ x * sin(4 * x)
+ }
>
> curve(g, 0, 3)
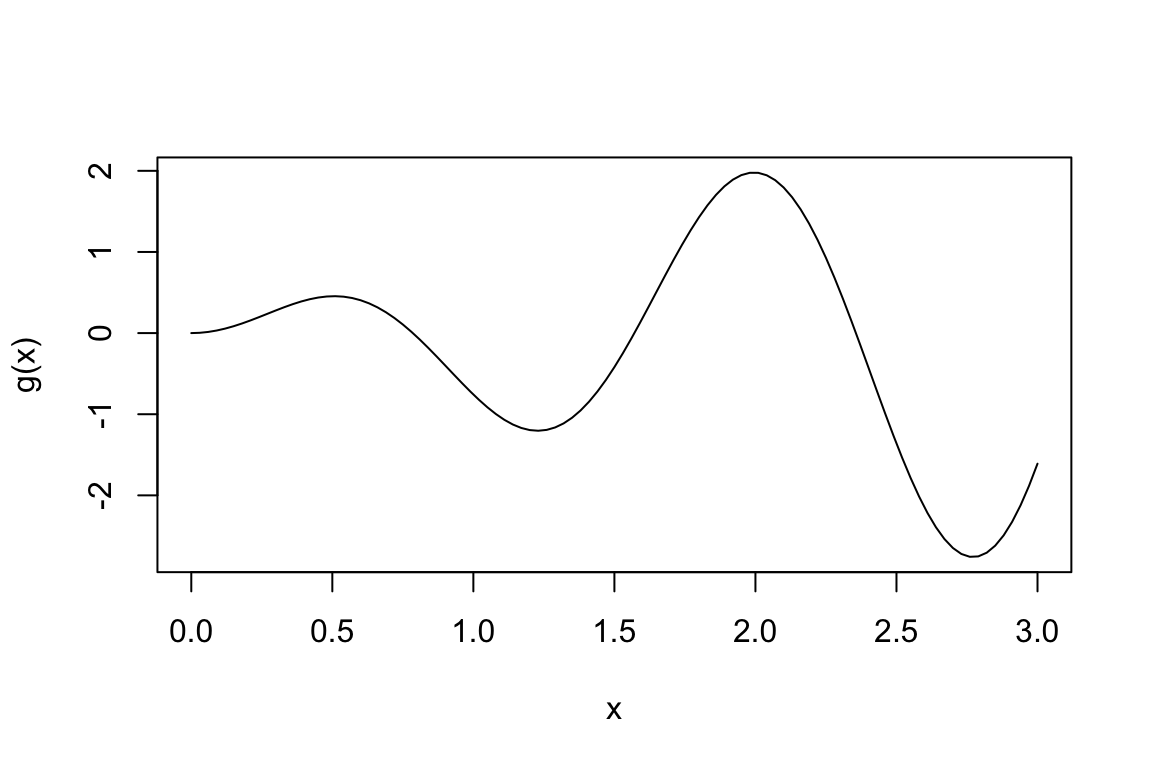
>
> # the algorithm gives the first minimum encountered
> optimize(g, c(0, 3))
## $minimum
## [1] 1.228
##
## $objective
## [1] -1.204
>
> # excluding the first minimum...
> optimize(g, c(1.5, 3))
## $minimum
## [1] 2.771
##
## $objective
## [1] -2.76
>
> # to find the global maximum
> optimize(g, c(1, 3), maximum = TRUE)
## $maximum
## [1] 1.995
##
## $objective
## [1] 1.979
>
> # or...
> minusg <- function(x) {
+ -g(x)
+ }
> optimize(minusg, c(1, 3))
## $minimum
## [1] 1.995
##
## $objective
## [1] -1.979
>
> # to find the global minimum
> curve(minusg, 0, 3)
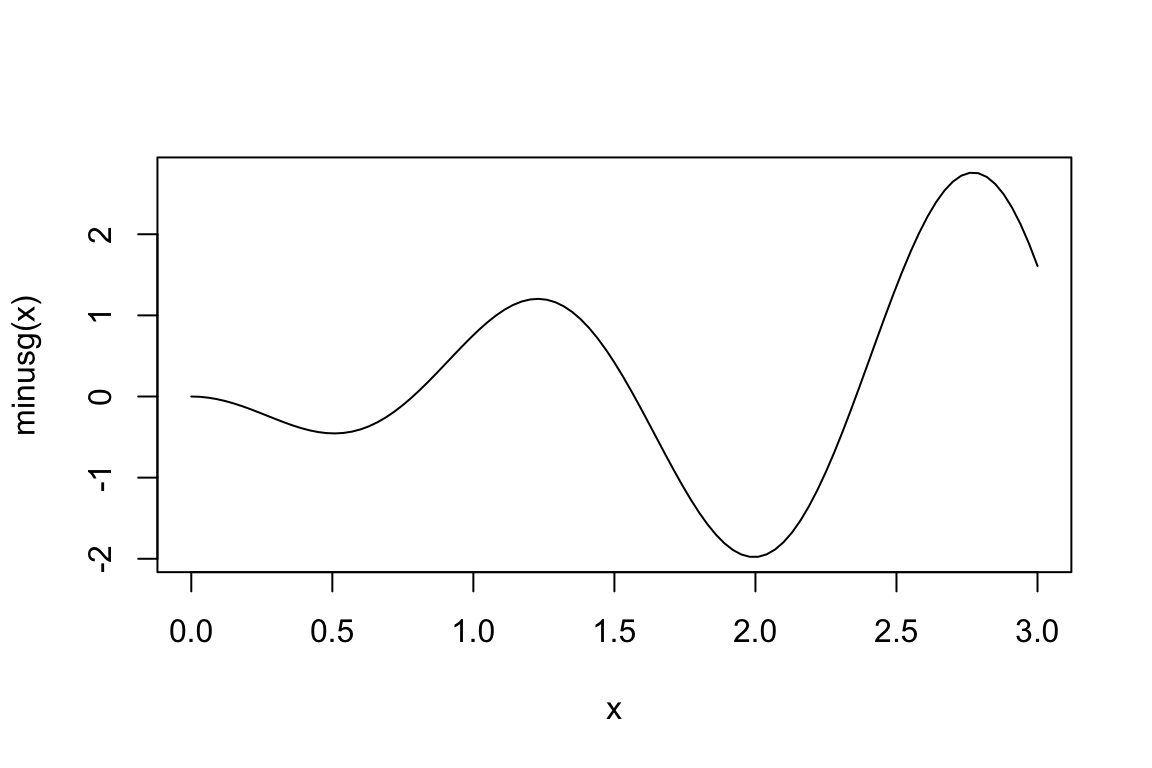
> optimize(minusg, c(1, 3), maximum = TRUE)
## $maximum
## [1] 2.771
##
## $objective
## [1] 2.76
- The
pracma package contains the function findmins(), which finds the positions of all the minima in the search interval:
> library(pracma)
##
## Attaching package: 'pracma'
## The following objects are masked from 'package:magrittr':
##
## and, mod, or
> curve(g, 0, 3)
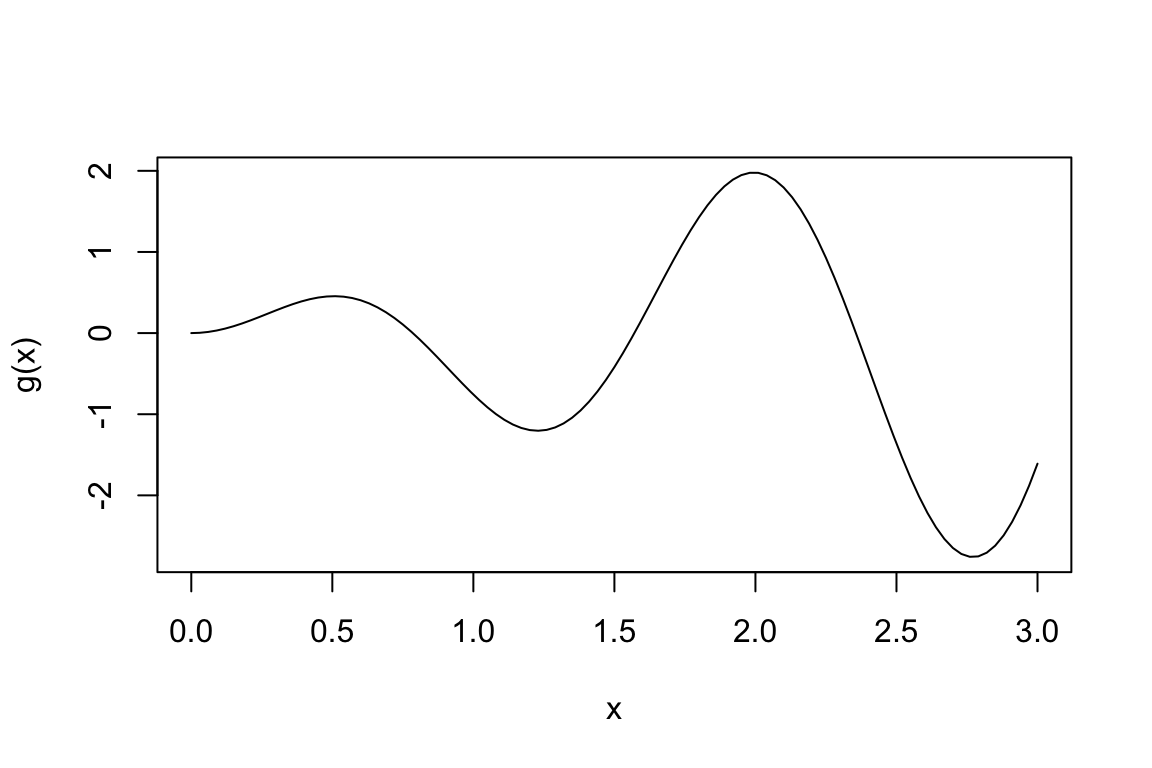
>
> g.mins <- findmins(g, 0, 3)
> g.mins # minima values
## [1] 1.228 2.771
>
> g(g.mins) # minima values
## [1] -1.204 -2.760


